【看中国2022年4月1日讯】1956年,物理学家约翰-凯利(John Larry Kelly),在《贝尔技术期刊》上,发了一篇题为“信息比例新解(A New Interpretation Of Information Rate)”的论文。

物理学家约翰-凯利(John Larry Kelly。作者博客)
在这篇论文中,凯利提出了一个如何处理信息传输中信号和噪音的公式,这就是后来大名鼎鼎的“凯利公式(Kelly Formula)”:
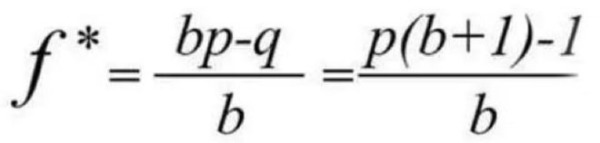
其中:f为信号发射端每次发送信号占总信息量的比率;p为接收端接收到有效信号占总信息量的比率;q为接收端接收到噪音信号占总信息量的比率,q=1-p;b为特定介质在信息传输过程中的信噪比(信号与噪声的比值)。
这篇论文,看上去科学严谨又高大上,但实际上完全不是那么回事儿——因为,这个公式是凯利在研究一个赌博游戏时琢磨出来的。
当时有一档电视答题节目正在热播,名叫《64000美元的问题》,因为节目火爆,就有人赌哪位选手能获胜。赌徒们能够提前获取一部分选手的信息,但这些信息有限而且可能有误,赌徒需要在不完全信息下进行下注。
凯利了解到这个赌局之后,就开始琢磨,如何利用有限的信息来参与赌博,才能在保证永远不输完的情况下,实现“利润最大化”?
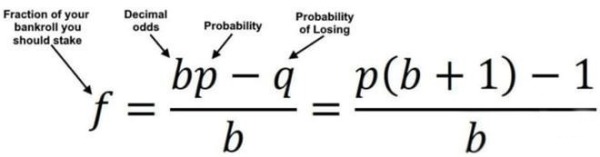
经过反复的推导,凯利总结出来了如下公式:
凯利公式的投资意义(作者博客)
其中的f,为计算出来的赌金最优投资比例,b为赔率,即期望盈利/预计亏损,p为成功概率,q为失败概率即1-p。
举个例子,假设一个抛硬币猜正反的简单赌局,每局赌注1元,猜中了得2元,猜错了输掉1元,也就是赔率b=2,胜率p=0.5,代入公式后算得f=0.25——也就是说,在这样一个简单抛硬币赌局中,如果能够无限次重复,每次投入所持有本金的25%,可以在永远不输光本金的前提下实现收益的最大化。
从这个公式里可以得出来两个推论:
1)除非胜率是100%,否则任何赌局都不能all in;
2)f为正值的赌局才值得参与,f为0或负值的游戏,重复参与的人必输无疑。
别人的一个赌博游戏,凯利能总结出如此简洁的数学公式,由此可见凯利之聪明。凯利此人不仅长得帅,聪明,还特别有趣。在加入贝尔实验室之前,他是美国海军的飞行员,加入贝尔实验室之后,他还加入了枪械俱乐部,又和妻子组队打桥牌锦标赛,还给敞篷车装上弹射座椅……
不过,在当时的贝尔实验室:
凯利的帅,只能排第二位;
凯利的聪明,也只能排第二位;
凯利的有趣好玩,还是只能排第二位。
以上三项,都稳排在第一位的那个家伙,叫香农(Claude Elwood Shannon)。

贝尔实验室的克劳德-香农(作者博客)
很多人可能没听说过这个人。但其实,香农是当代信息论的开山鼻祖。他的硕士论文以及后来发表在《贝尔技术期刊》上的两篇论文,确立了当代通信编码的基本原理,他用数学公式来描述通信定理,为信息论和数字通信奠定了基础。正是沿着他的思路,才有了今天的互联网世界。
某种程度上说,现在的我们,能够在互联网上自由地即时聊天、打电话、听音乐、看电影等等,其实都应该感谢他。
话说凯利总结出这个公式后,就拿给香农看,香农建议他写成文章。起初,题目是“信息理论与赌博”,但贝尔实验室的东家AT&T担心,大众可能认为实验室在拿着研究资金搞非法赌博,所以在发表时名字特意改成了“信息比新解”。
凯利公式发表后,一直没有激起什么特别的浪花,直到被一个叫爱德华-索普(Edward O.Thorp)的家伙给看到。
索普这人,从小就是个数学计算神童,28岁就在著名的麻省理工学院当了数学讲师。但他从小就喜欢研究赌博,一直想要找到一种方式,通过大量的数据计算,来预测轮盘赌中弹珠最后的大致位置。
1960年,索普大致完成了自己的猜想,他想将论文发表在美国科学院院刊上,但这个刊物规定,必须由科学院院士推荐或署名才行。于是,索普就找到了当时麻省理工唯一的国家科学院院士——香农。
香农一直都是个老顽童,索普的这种主意很快就打动了他,他同意推荐论文发表,然后,按照索普的理论,两个人一起制造了一个简易的计算器,到各个轮盘赌上去小试身手。结果发现,因为各种计算误差,赌博成果一直都差强人意。
这个时候,香农忽然想起来凯利公式,就把这篇论文,推荐给了索普,索普一眼就看了出来,这个公式可以应用到当时各大赌场盛行的21点赌博游戏中——该游戏由2到6个人玩,使用除大小王之外的52张扑克牌,游戏者的目标,是使手中的牌的点数之和不超过21点且尽量大。
为了验证凯利公式和“数牌法”在实际中的效果,索普于是约了一个专业赌徒,拿着1万美元的本钱,到附近的两个小赌场里小试身手,结果,仅一个周末里,就狂赚1.1万美元。
确认策略有效后,索普联合香农,设计了史上第一个便携式“计算器”。接下来,一旦没钱花了或者手痒难耐的时候,索普就和香农及夫人在周末坐上飞机,飞往拉斯维加斯,在赌场里大玩21点,挣一大把钱后走人。

投资达人爱德华-索普(作者博客)
由于索普在赌场中屡屡获胜,不久就被各大赌场列为“不受欢迎的人”。为了能继续赢下去,索普使用了化妆术,后来干脆雇佣别人代替他本人去赌博,但赌场也越来越警惕。
索普的名声在赌博业里传开了,很多人都想学这种方法。索普干脆从挖金子改行卖铲子,于是在1962年写了一本书:《战胜庄家:21点中的获胜策略》(Beatthe Dealer: A Winning Strategy for the Game of Twenty-One),详细披露了自己是如何在赌场中赚钱的。
这本书迅速登上纽约时报畅销书排行榜,销量高达70万册,比索普本人化妆去辛苦赌博挣钱多多了,这也证明了一个真理:卖铲子比挖金子赚钱。
那我们来看看,索普到底是怎么在21点的赌博中挣钱的呢?
其实很简单,记牌!
因为21点是扑克牌游戏,而每一副牌中某花色或点数的总量是一定的,每一轮赌博过后,发牌员手中的牌数就会减少。通过记下已经出现的牌,索普就能计算发牌员手中有什么样的牌,然后根据这些牌的花色、点数估算出现不同情况的概率,进而用凯利公式来计算下注比例。形势有利的时候就下大赌注,形势不利的时候就下小赌注。
那个时代赌场也很“笨”,一般只用1-2副牌,而且发牌员常常将牌发完之后才洗牌,导致记牌并非难事。索普公布了自己的办法之后,赌场就学精了,每次用6-8副牌,而且发牌不到1/3就重新洗牌,而且禁止携带电脑和数牌的电子设备进场,基本就堵上了这个漏洞。
索普的书畅销了之后,凯利公式开始变得世人皆知,甚至有人称之为“财富公式”。
到了1969年,一个年轻的纽约证券经纪人里根找到了索普,希望和索普一起成立一个对冲基金,将索普的理念和方法完全商业化。索普可以继续做他的研究,并作为基金经理下交易指令,而里根帮助他做产品销售,客户维护,完成交易执行以及其他所有的琐事。
从1969年成立,到1988年因诉讼而意外停业,索普的基金20年年化收益率19.1%。虽然在投资大师里貌似不算惊人,但如果你查看该基金净值会发现,近20年的跨度下,该基金居然没有一年亏损,共计230个月,只有3个月有回撤,且回撤幅度全部小于1%——这,大概是有史以来“最完美的投资曲线”。
实际上,索普的基金,是美国第一只完全的中性策略基金,仅基于数学计算的概率和市场的定价失误进行投资,即使在1987年的美股暴跌中,索普的基金也基本保持稳定,到年末,甚至还赚了大钱。
随着参与到华尔街的“大赌博”中来,索普见了许多投资界人士,其中有一个叫巴菲特。那个时候他还不是股神,但两人交流之后惺惺相惜,索普甚至预言,巴菲特会成为美国最富有的人。多年之后的巴菲特,的确实现了索普的预言。
索普认为,巴菲特是真正的投资大师,所以他把自己相当一部分财富,入股了巴菲特的公司,成为巴菲特的早期股东之一,这些股份一直持有到现在。
1994年,索普重新成立了一家对冲基金,这个基金业绩更好,可惜到2002年他也主动解散——外部原因来说,是对冲基金数量激增,交易机会减少,但更重要的原因,是索普对赚钱的兴趣降低了,他觉得和家人在一起,才是更好的时光。
索普对名声也并不在意,后来震动了整个投资界Black-Scholes期权定价模型,其实索普自己早已推导出来,但他的选择是自己默默挣钱。后来,这个公式的两位作者布莱克(Black)和斯科尔斯(Scholes),还特意在论文里感谢索普的贡献。
索普对此很平静:“我从未考虑过我的荣誉,因为我不是从事经济学和金融行业研究的人,这个问题附带的重大意义并不在我的思考范围。”
相比于索普研究的个人化和隐私化,BS期权定价模型让每个投资者都可以预测期权价格,它的提出彻底颠覆了以往的金融运行体系,华尔街的量化投资时代正式到来了。到了后来,麻省理工教授罗伯特-默顿(Robert Merton)采用随机微积分将公式进一步完善,他和斯科尔斯共同获得了1997年的诺贝尔经济学奖。
所以,某种程度上说,索普是当今所有量化投资的鼻祖。
实际上,当前金融市场上叱咤风云的知名对冲基金经理,几乎都在使用凯利公式进行投资,这其中包括比尔-格罗斯(Bill Gross,债券投资之王)、詹姆斯-西蒙斯(James Simons,文艺复兴公司名誉主席、世界级的数学家)和投机之王乔治-索罗斯(George Soros)等人。
特别值得一提的是,索普不再做对冲基金后,偶尔会做一些基金管理咨询的事情,结果他就发现,伯纳德-麦道夫的证券投资公司大有问题,劝朋友把钱撤出来。果不其然,2008年的时候,这一美国历史上最大的“庞氏骗局”被揭露,诈骗金额超过600亿美元。
索普写了一本自传《A Man For All Markets》,这里的All Markets,意思是,他涉及了几乎所有的交易市场,从赌场到华尔街,OTC期权、可转债、股票、期货等……
另外,如今在美国量化对冲基金领域鼎鼎大名的TGS基金,据说就是索普的三个徒弟一起创办的,而TGS中的“T”,就是Thorp的名字。
